OpenGL and Direct3D Perspective Matrix

Perspective Matrix Four Ways



The Perspective Matrix is vital to 3d graphics. It's the final matrix responisble for projecting a 3d object from the world onto a flat screen. Unlike the other two common matrices used in 3d graphics: the Model Matrix (resposible for moving the vertices from Model to World Space) and View Matrix (responsible for moving the vertices from World to Camera Space), the perspective matrix can be hard to intuitively understand. Specifically the the Z-Axis transformation to prepare it correctly for the z-divide.


Adding to this is the different orientations of the axis used in the 3d game world. There are two common orientations - the so called left hand and right hand coordinate orientations. The positive X axis pointing right, the positive Y axis pointing up but the positive Z-axis pointing into the screen (Left handed) or the positive Z-axis pointing out of the screen (Right Handed coordinate system). Although these are the two most common coordinate systems there are 4 possible unique 3d orientations that a game world could use. This means 4 different perspective matrices to map the game world onto a flat screen. This is only for one graphics API. The number of matrices increase by the number of graphics API's with their own internal coordinate systems (NDC space) that you have to convert to.



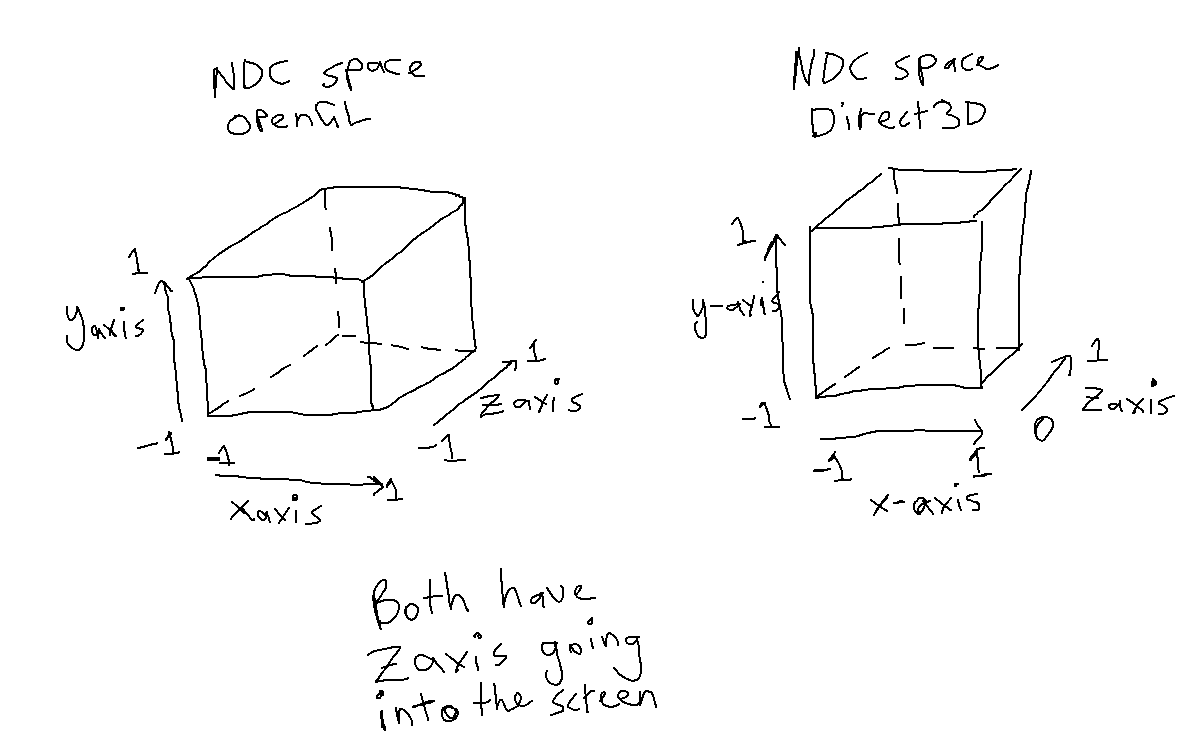
In OpenGL NDC space, the coordinate system is Left-Handed (the z axis pointing into the screen). Direct3D is the same, but the Z-Axis origin is in a different place. In Opengl the Z-Axis ranges from -1 to 1, in Direct3D the Z-Axis ranges from 0 to 1 (both pointing into the screen).


On top of this, there is one more thing to take into consideration that also affects the perspective matrix: the order we are multiplying it in the shader (order of operations).


Contents


Three factors we have to take into account


4x4 Matrix Struct defined in code


Same Code for all the Perspective Matrices


Matrix 1


Matrix 2


Matrix 3


Matrix 4


Orthographic Matrices


Same Code for all the Orthographic Matrices


Matrix 5


Change the X Y origin of window


Matrix 6


Matrix 7


Matrix 8


Order of Operations


Conclusion


Notes


Three factors we have to take into account


So there are three factors that contribute to the possible perspective matrices you could have:


1. The coordinate system orientation of the Game World.


2. The coordinate system of the GPU API your're using (NDC Space)


3. The order of operations we are doing our matrix multiplications in the shader


So to build the right perspective matrix, you have to be aware of all three of these things. For simplicity I'll only be looking at left and right handed game world coordinate systems (the two most common ones) and the two graphics APIs: OpenGL and Direct3D. I'll also assume we're writing the order of multiplications like you'd see in Math, going from right to left. I won't be deriving the matrix, just showing you the matrix and how you'd define it in code so you can see the differences.


4x4 Matrix Struct defined in code


Our matrix struct will look like this:


struct Matrix_4x4 {
float E[16];
};

Just 16 floats side by side in memory. Our job is to fill the right values in.


Same Code for all the Perspective Matrices


All the perspective matrices will be using the same data to build the matrix.


//NOTE: The Field of View the camera can see in degrees
float FOV_degrees = 60.0f;

//NOTE: Our Near and Far plane constants
float nearClip = 0.1f;
float farClip = 1000.0f;

//NOTE: Convert the Camera's Field of View from Degress to Radians
float FOV_radians = (FOV_degrees*PI32) / 180.0f;

//NOTE: Get the size of the plane the game world will be projected on.
float t = tan(FOV_radians/2); //plane's height
float r = t*aspectRatio; //plane's width


We have the Near and Far clip plane constants that may be something like 0.1 and 1000 respectively. This defines the min and max bounds of what is visible on the Z-Axis.


We then have the Field of View (FOV) of the camera in the game world. It is how much of the world in the X and Y axis the camera can see at once. We convert it to radians.


We divide the FOV by 2 since the FOV is the angle for the whole camera view (the whole viewport) but we just want half since the x,y origin is in the middle of the screen. The FOV is assumed for what the camera can see in the Y-Axis. We use the aspect ratio of the viewport to get the size of the projection plane in the X-Axis. (You could just as easily have the field of view be defined as what the X-Axis can see and use the aspect ratio to get the Y-Axis size).


The near and clip plane aren't negated based on the whether the game axis orientation is left handed or right handed. They are always positive.

Matrix 1: OpenGL for Left Handed Orientated Game World (Camera looking down the Positive Z-Axis)


Matrix_4x4 result = {{
1 / r, 0, 0, 0,
0, 1 / t, 0, 0,
0, 0, (farClip + nearClip)/(farClip - nearClip), 1,
0, 0, (-2*nearClip*farClip)/(farClip - nearClip), 0
}};


You'll notice it has the 1 in the 4th column, 3rd row which allows for the divide by Z the graphics card will do for us that makes the world have perspective (as opposed to orthographic). The 1 is positive since the Z-Axis in the game world is the same direction as the Z-Axis in OpenGl's NDC space (positive Z going into the screen).


Matrix 2: OpenGL for Right Handed Orientated Game World (Camera looking down the Negative Z-Axis)


Matrix_4x4 result = {{
1 / r, 0, 0, 0,
0, 1 / t, 0, 0,
0, 0, -((farClip + nearClip)/(farClip - nearClip)), -1,
0, 0, (-2*nearClip*farClip)/(farClip - nearClip), 0
}};


You'll notice the 1 value in the 4th column, 3rd row is now negative. Also the Z-component of the matrix (3rd Column, 3rd Row) is also negative now too. This is in order to flip the Z-Axis. You can't just have the z-component (3rd Column, 3rd Row) negative since then the homogenous value of the resulting vector (w component) would be neagtive and we would divide the X and Y by a negative value, flipping them aswell. So we want to the 1 value in the 4th column, 3rd row to also be negative.


Matrix 3: Direct3D for Left Handed Orientated Game World (Camera looking down the Positive Z-Axis)


Matrix_4x4 result = {{
1 / r, 0, 0, 0,
0, 1 / t, 0, 0,
0, 0, farClip/(farClip - nearClip), 1,
0, 0, (-nearClip*farClip)/(farClip - nearClip), 0
}};


For the Direct3D matrices the origin of the Z-Axis in NDC space is at zero not negative one. To account for this, we no longer multiply the Z-Translation component(3rd Row, 4th Column) by 2 and the Z-Component(3rd Row, 3rd Column) value has also changed.


Matrix 4: Direct3D for Right Handed Orientated Game World (Camera looking down the Negative Z-Axis)


Matrix_4x4 result = {{
1 / r, 0, 0, 0,
0, 1 / t, 0, 0,
0, 0, -farClip/(farClip - nearClip), -1,
0, 0, (-nearClip*farClip)/(farClip - nearClip), 0
}};


We've now added in the negative values to flip the positive Z-axis from pointing out of the screen to into the screen (Same as what we did with the OpenGL matrix).


That's it. The four most common perspective matrices you'll come across in game programming. It should be noted that these matrices assume the near clip plane is also the distance of the projection plane from the camera's eye. This doesn't have to be the case: the distance of the plane can be decoupled from the near clip plane, although this is less common and doesn't hold any significant advantages.


Orthographic Matrices


Above are all perspective matrices where all the light rays are coming into a single point: the centre of the camera. The other type of matrix you'll come across in graphics programming is the Orthographic Matrix where all the light rays hiting the camera are parallel to each other . This is handy for doing GUI programming, game UI or making a program like a text editor that doesn't need perspective. Just like there are 4 perspective matrices to account for the two game world orientations and two Graphics APIs, there are also 4 Orthographics matrices for the same cases. I'll outline them now.


Same Code for all the Orthographic Matrices


//NOTE: The size of the plane we're projection onto
float a = 2.0f / screenWidth;
float b = 2.0f / screenHeight;

//NOTE: Near and Far Clip plane
float nearClip = 0.1f;
float farClip = 1000.0f;

//NOTE: We can offset the origin of the viewport by adding these to the translation part of the matrix
float originOffsetX = 0; //NOTE: Defined in NDC space
float originOffsetY = 0; //NOTE: Defined in NDC space


The near and clip plane aren't negated based on the whether the left handed or right handed coordinate system is being used. They are always positive.

Matrix 5: OpenGL Orthographic Matrix For Left Handed Orientation (Positive Z-Axis into the screen)


Matrix4 result = {{
a, 0, 0, 0,
0, b, 0, 0,
0, 0, (2.0f)/(farClip - nearClip), 0,
originOffsetX, originOffsetY, -((farClip + nearClip)/(farClip - nearClip)), 1
}};


You'll see the homgenous cooridinate value (4th column, 3rd row) is now zero. Since we don't want to divide by the z-coordinate with a orthographic projection, we want the resulting w coordinate to be a 1. So we put a 1 in the 4th column, 4th row. (If we didn't do this, the w component of the resulting vector would be zero, and the graphics card would try dividing the x, y, z values by zero which is not good!).


Change the X Y origin of window


We also have the ability to change where we want the origin of the incoming vertices to be. This is handy if we want to render as if the bottom-left corner of the window is origin. To do that we would change the origin offset values:


//NOTE: Change the origin to the bottom-left corner of our Viewport
float originOffsetX = -1; //NOTE: Defined in NDC space
float originOffsetY = -1; //NOTE: Defined in NDC space

We could also move the origin of the window to the top-left hand corner which might be handy for text rendering:


//NOTE: Change the origin to the top-left corner of our Viewport
float originOffsetX = -1; //NOTE: Defined in NDC space
float originOffsetY = 1; //NOTE: Defined in NDC space

Matrix 6: OpenGL Orthographic Matrix For Right Handed Orientation (Negative Z-Axis into the screen)


Matrix4 result = {{
a, 0, 0, 0,
0, b, 0, 0,
0, 0, -(2.0f)/(farClip - nearClip), 0,
originOffsetX, originOffsetY, -((farClip + nearClip)/(farClip - nearClip)), 1
}};


The only difference in this Right Handed Orientation is the negative sign on the Z-component of the matrix (3rd Column, 3rd Row), flipping the incoming z values. We don't have to negate the 1 value in the far right column like in the perspective version, since this time the w component of the resulting vector won't have the incoming z value, it will just stay 1.


Matrix 7: Direct3D Orthographic Matrix For Left Handed Orientation (Positive Z-Axis into the screen)


Matrix4 result = {{
a, 0, 0, 0,
0, b, 0, 0,
0, 0, 1.0f/(farClip - nearClip), 0,
originOffsetX, originOffsetY, nearClip/(nearClip - farClip)), 1
}};


We account for the origin shift in Direct3D.


Matrix 8: Direct3D Orthographic Matrix For Right Handed Orientation (Negative Z-Axis into the screen)


Matrix4 result = {{
a, 0, 0, 0,
0, b, 0, 0,
0, 0, -1.0f/(farClip - nearClip), 0,
originOffsetX, originOffsetY, nearClip/(nearClip - farClip)), 1
}};


Same as above but we flip the incoming z values.


Order of Operations


These matricies could just as easily been written as their transpose looking like this for Matrix 3:


Matrix_4x4 result = {{
1 / r, 0, 0, 0,
0, 1 / t, 0, 0,
0, 0, farClip/(farClip - nearClip), (-nearClip*farClip)/(farClip - nearClip),
0, 0, 1, 0
}};

You may come across this layout in people's code. If you do this, you have to account for it with your order of operations done in the shader.


GLSL



So our Model View Projection calculation would look like this in glsl with the matrices layout in this article:


vec4 position = Projection * View * Model * vec4(incoming_vertex_vec3, 1.0);

If we took the transpose of our matrices, we would also have to flip the order of operations in our shader code. So it would look like this:


//NOTE: We've flipped the order of matrix multiplies
mat4 position = vec4(incoming_vertex_vec3, 1.0) * Model * View * Projection;

HLSL



In hlsl with the original layout of the matricies in this article:


float4 position = mul(Model, float4(incoming_vertex_vec3, 1.0f));
position = mul(View, position);
position = mul(Projection, position);

And if we took the transpose of them:


float4 position = mul(float4(incoming_vertex_vec3, 1.0f), Model);
position = mul(position, View);
position = mul(position, Projection);

The mul function will change the incoming vector as a row or column vector based on whether you pass it as argument 1 or 2 👆


Depending on how you want to write your matrix multiplication in your shader, you have to match it with the way you layout you matrix in memory.


Conclusion


Hopefully this wil be a handy reference when implementing the perspective matrix in your program. We covered the four most common perspective matrices you'll come across aswell as showing the orthographic versions.


Notes


[1] These matrices and information is taken from 3D Math Primer for Graphics and Game Development (2nd Edition) by Fletcher Dunn and Ian Parberry in Chapter 10


[2] You can see the derivation of the perspective matrix here. This is building a matrix like Matrix 4 in the article.